This page contains some research projects
See individual faculty webpages for more projects.
Graph Pebbling
Faculty: Glenn Hurlbert
Graph Pebbling is a network optimization model for the transportation of resources that are consumed in transit. Electricity, heat, or other energy may dissipate as it moves from one location to another, oil tankers may use up some of the oil it transports, information may be lost as it travels through its medium, or military troops may be lost while moving through a region. The central problem in this model asks whether discrete pebbles from one set of vertices can be moved to another while pebbles are lost in the process. A typical question asks how many pebbles are necessary to guarantee that, from any configuration of that many pebbles, one can move a pebble to (“solve”) any particular vertex. A fractional version asks for the limiting behavior of the average number of pebbles used per “solution”. Instead of placing the initial pebbles cleverly, if the original configuration is chosen at random then we can wonder what the probability is that every vertex can be solved, which gives rise to the notion of a threshold, which divides almost sure success and almost sure failure. One may also ask: how few pebbles can be used so that, from some configuration of that many pebbles, one can move a pebble to any particular vertex; how many pebbles are required to guarantee that, from any configuration of that many pebbles, some pebble can travel at least some fixed distance; and other questions. Various rules for pebbling steps have been studied for years and have found applications in a wide array of areas: computational complexity theory (time-space tradeoffs), optimal register allocation for compilers, pursuit and evasion games (e.g. combating computer viruses), graph searching, computational linear algebra (Cholesky factorization of large sparse matrices), computational geometry (rigidity of graphs, matroids, and other structures), combinatorial number theory and combinatorial group theory (zero sum theory), and p-adic diophantine equations. Most of these rules give rise to computationally difficult problems. Currently I am working on conjectures related to structured graphs such as chordal graphs. There are many, many open problems in this area for interested students to work on.
Universal Cycles
Faculty: Glenn Hurlbert
A deBruijn cycle of order n is a cyclic listing of 0s and 1s with every binary n-tuple appearing exactly once contiguously in the cycle. A Gray code is a listing of all binary n-tuples so that adjacent n-tuples differ by just one bit. Both of these are examples of Universal Cycles, listings of combinatorial objects that are efficient for various applications in Communications, Cryptography, Randomization, Computer Science, and elsewhere. Recently there has been much work on these in the area of Combinatorial Designs, which are important in Statistics, in addition to the above. There are a number of outstanding questions to answer, and a new book (Ordering Block Designs, by Dewar & Stevens) that outlines the current frontiers.
Intersection Theory
Faculty: Glenn Hurlbert
From a population of n people, how many committees can be formed so that every pair of committees share a common member? What if the size of each committee is fixed, or is even (or is odd)? What if each committee must share k members? What if, instead of committees (subsets) of people (elements) we ask about other combinatorial structures such as partitions or permutations of a set, or subspaces of a vector space, etc? These are all basic questions in intersection theory, a specialty within extremal set theory and combinatorics that has fundamental applications to wide ranging disciplines such as polynomial algebra, probability, group theory, circuit complexity, statistics, number theory, graph coloring, geometry, and more. Recently I have been pursuing questions regarding independent sets in graphs (especially in trees), as well as the following 1972 conjecture of Chvatal: if F is a family of sets that is closed under taking subsets then the largest intersecting subfamily of F consists of those sets of F that contain some fixed element.
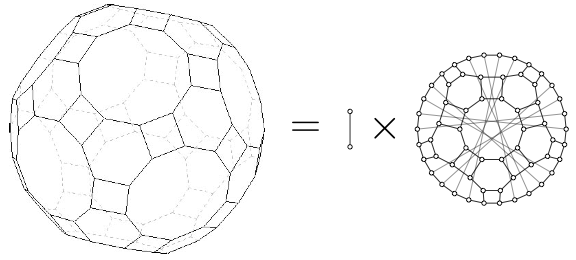
Algebraic Operations on Graphs
Faculty: Richard Hammack
My primary research interest is in graph theory, a highly visual branch of mathematics concerned with networks of interconnections between nodes. I am especially fascinated by algebraic operations on graphs. For example, there are various ways to multiply graphs together to get new graphs, or, conversely to factor a given graph into a product of smaller graphs. This leads to many questions: Do graphs factor uniquely into prime graphs, the way that numbers factor uniquely into prime numbers? If A × C = B × C for three graphs A, B and C, can we conclude A = B? Can you divide one graph into another? What would it look like? There are fascinating answers to such questions, as well as many, many unsolved mysteries.
The research that I have done with students has led to about 10 published papers so far.
Graph Coloring
Faculty: Dan Cranston
Collaborators: Landon Rabern
For a graph G, we write χ(G), Δ(G), and ω(G) for the chromatic number, maximum degree, and clique number of G. Brooks showed that χ(G) ≤ max{ω(G), Δ(G)}, when Δ(G) ≥ 3. Borodin and Kostochka conjectured that χ(G) ≤ max{ω(G), Δ(G)-1} when Δ(G) ≥ 9. If true, this is best possible. We have proved this conjecture for claw-free graphs (those with no induced K1,3). The contrapositive of the conjecture says that if Δ(G) ≥ 9 and χ(G) ≥ Δ(G), then ω(G) ≥ Δ(G). In this direction, we showed that if Δ(G) ≥ 13 and χ(G) ≥ Δ(G), then ω(G) ≥ Δ(G)-3.
Graph Brain Project
Faculty: Craig Larson
Craig Larson and Nico Van Cleemput (Ghent University) have developed the Conjecturing program which can produce conjectures in any area of mathematics. Graph Theory is defined in part by its published concepts (invariants and properties), examples and counterexamples, theorems, and open problems.
One goal of this project is to code all published concepts, examples and counterexamples, and theorems. This is a long-term, massive project, which will ultimately require the work of a community of interested researchers.
As we add published graph theory knowledge we will continually propose experiments and investigate how advancing knowledge allows our program to advance research on existing graph theory problems.
Some of our experiments have included generating invariant and property conjectures in a variety of mathematical domains, developing a conjecture-based sequence guessing program, a conjecture-based Chomp playing program, as well as a conjecture-based program for classification of objects from their features. The possible experiments are limited only by your imagination!
2107 Graph Brain Project summer research project.
Sensory Inputs and Fluctuations in Cortical Neural Networks
Faculty: Cheng Ly

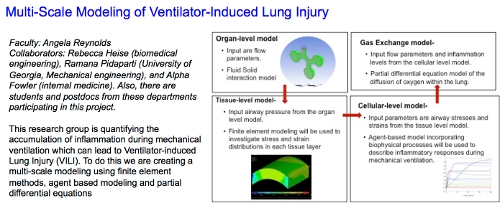
Multi-Scale Modeling of Ventilator-Induced Lung Injury

Pollen Dispersal
Faculty: David Chan
Collaborators: Rodney Dyer (VCU)
We are studying pollen movement through insect dispersal in dogwood at the VCU Rice Center for Environmental Research. In this project we are developing a variety of models and performing several experiments to better understand the behavior of insects in dispersing pollen. Gene movement within a plant population in a complex process and also critical for sustaining species in not only forests but also in agricultural and urban environments.